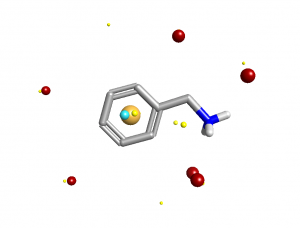
如何计算带电分子周围的静电环境

我们经常被问到的一个问题是：”你如何处理带电分子？” 这与小分子非常相关，但在另一个常问问题中变得至关重要：”你能把场放到蛋白质上吗？” 这里我们详细介绍了处理带电小分子的方法和原理。

计算分子周围某一点的静电场值

为了计算分子周围某一点的静电场值，我们在该位置放置一个带电的”探测原子(probe atom)”并测量其相互作用能。这种计算只是近似的：对于适当的能量，我们必须允许分子对探测原子做出响应然后再重新极化。 Cresset的XED力场包含了原子极化率，但是如果我们对于每个假定的场点位置重新极化配体，计算将太慢。为了给出良好的场模式力场的参数化考虑了这一点。

这种场计算算法对于大多数中性小分子工作地非常好，并且我们在参数化XED力场中使用的标准之一是确保以这种方式计算的场电势尽可能地匹配实验确定的分子相互作用能量和几何形状。然而，有两个潜在的症结我们必须处理：电介质和形式电荷。

蛋白质中配体的介电常数是多少？

电介质问题是一个有趣的问题。我们主要对充当配体的分子感兴趣，即，它们与某种生物大分子相互作用，通常是蛋白质。我们期待配体分子周围有什么样的环境？在真空中进行计算，最简单的解决方案显然是不合适的。然而，最常用的替代方法是应用某种溶剂化静电模型来模拟水环境(GBSA、Poisson-Boltzmann等)也是不合适的，因为当我们的配体被水完全溶解时，我们并不真正关心它的外观，因为蛋白质并不是这样看待它的。蛋白质活性位点内部的有效电介常数难以准确测量：对于干的蛋白粉末，一般接受的值似乎在2-5左右，溶剂化蛋白质的活性位点的值在1-20或更大。^[1,2] 酶活性位点内部的介电常数似乎在10左右，但这可能受到来自蛋白质表面上的移动电荷残基的强贡献的影响。^[3]

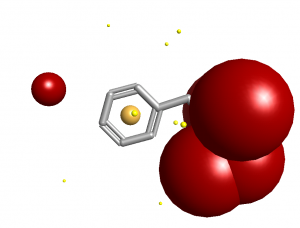
考虑到这一切，对于配体假设什么介电环境的问题比通常假设的更复杂。我们花了很多时间研究这个问题，并且发现假设配体周围的简单电介质为4似乎给出了很好的结果。这大致上适合于中等包埋的活性位点，但对于高度暴露的活性位点肯定太低。实际上，它似乎对中性分子有很好的作用，但对带电分子又有什么作用呢？使用简单介电常数4导致带电基团完全支配了分子的静电–而不是描述其结合特性的精细场模式，你只会得到一个大的电荷球（右）。应该注意的是，常用的计算水中泊松-玻尔兹曼（Poisson-Boltzmann）静电方法在小分子中也会遇到同样的问题：分子内部的低介电常数(相对于其周围的高介电质)允许局部形式电荷支配分子的静电。

我们的方案

我们有两个假设：生物系统中的相互作用倾向于在高离子强度下发生，带电配体通常（尽管不总是）倾向于与蛋白质中的带电残基相互作用。它们很少直接与结合口袋的非常疏水/低介电区域相互作用。由于配体周围确切的蛋白质环境通常是未知的（如果是的话，那么首先就不需要使用基于场的叠合了！），我们通过假设带电基团通常在附近某处具有反离子或移动溶剂化壳来近似这些效应，因此它们平均经历比分子的非带电区域更高的介电常数。大量的测试表明，设置有效介电常数为32工作得很好，因此我们所有的场计算都在分子中性部分的介电常数为4、带电基团的介电常数为32的情况下进行的。这对场的影响是带电基团具有大的场点，如你所期望的，但不会从分子的剩余部分吸收静电势。

结论

所以我们有一个可行的方法来解决介电问题，至少对于小分子。回到另一个问题，”我们能给蛋白质添加场模式吗？” 从计算的角度来看，答案是”是的”，尽管计算很慢。然而，如果你考虑介电问题，你很快就会发现将同样的场计算方法应用于配体和蛋白质是有根本缺陷的。我们的标准场计算方法假定分子存在于无蛋白质的环境中。蛋白质不是这样的！我们一直在寻找非常有希望的替代方案，随着方法的发展，我们将在我们的博客和技术部分详细介绍这些方案。

文献

Nakamura et al., Protein Eng., 1988, 2(3), p177
Kukic et al., JACS 2013, 135(45), p16968
Mertz and Krishtalik, PNAS 2000, 97(5), p2081

原文：https://www.cresset-group.com/science/field-technology/how-to-calculate-the-electrostatic-environment-around-charged-molecules

编译：肖高铿